피타고라스율(영. Phytagorian scale, 도.Phytagoreische Stimmung)
기원전 550년 경 피타고라스는 현의 길이가 2:3인 완전5도를 연속적으로 연결하여 음계를 발명한 것으로 전해진다. 피타고라스율에서 모든 음의 주파수는 완전5도 관계에 의해 산출된다. 아래 그림을 보면 C음의 주파수를 1로 했을 때, 이보다 완전5도 위인 G는 3/2, G보다 또 완전5도 위인 D는 3/2의 제곱이 되며, 이런 방식으로 G까지 쌓아 올라갈 수 있다. 그리고 C보다 완전5도 아래인 F는 주파수가 2/3이 된다.

위의 일곱 개의 음은 바로 온음계의 7음인데, 이를 음계로 만들기 위해서는 모든 음들을 한 옥타브 안에 넣어야 한다. C의 주파수를 1로 했을 때 F는 C 아래의 F(2/3)보다 한 옥타브 위이므로 4/3, G는 3/2이다. 또한 D와 A는 한 옥타브씩 내려야 하므로 각각 9/8(9/4 : 2)과 27/16(27/8 : 2)이 된다. 한편 E와 B는 두 옥타브씩 내려야 하므로 각각 81/64와 243/128이 된다. 이를 다시 C로부터 시작하는 온음계로 정리해 보면 다음과 같다.

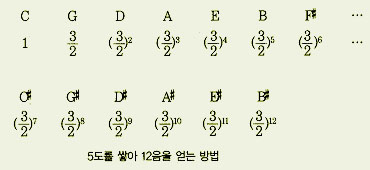
옥타브 내의 그 소우주의 척도로서 5도를 가진 피타고라스율은 선율적 목적을 위해서는 완벽한 것이다. 그러나 음역을 넓혀 5도를 계속 확장해 나가면 문제점이 드러난다. 예를 들어 5도를 12번 쌓으면 결국 반음계의 12음이 모두 등장하게 되고 마지막 12번째 음의 주파수는 주파수가 첫 음의 (2/3)의 12승 배가 될 것이다. 따라서 이 음의 주파수는 첫 음의 주파수 1의 “2의 7승배”가 되어야 마땅하다. 그러나 “(2/3)의 12승”과 “2의 7승”은 같은 수가 아니라는 문제가 생긴다. 이렇게 불일치한 숫자의 비율을 피타고라스의 콤마(Phythagorian comma)라고 한다.
등록일자:2005-11-29
이석원

