저자: 김미옥
등록일자: 2006-11-13
김미옥: 하모니론, 프톨레마이오스 [Harmonikē, Harmonics, Ptolemaios, Ptolemy]
프톨레마이오스(그. Ptolemaios, 영. Ptolemy, 알렉산드리아, 83년 이후〜161)의 저서. 저자는 그리스의 천문학자, 수학자, 지리학자, 음악이론가였다. 3권에 달하는 그의『하모니론』은 고대의 음악이론을 명확하게 정리, 보완한 것이다. 고대 그리스 선법을 7가지로 체계화한 첫 저작물로 알려져 있다.
이 책은 후대의 여러 이론가들에게 큰 영향력을 행사했다. 그 이론은 보에티우스(고대 말/ 중세 초)를 통해 전달되며, 르네쌍스 시대에는 라틴어로 번역되기도 했다(1562). 바로크 시대에 케플러(Johann Kepler, 1571〜1631) 등의 저서에도 인용되었다.
프톨레마이오스는 많은 수학적 비율을 사용한 점에서 피타고라스 학파에 속한다고 볼 수 있으나, 그 자신은 그 학파의 이론에 대해 일반적으로 현실과는 거리가 먼 것이라고 비판했다. 또한 그는 논리와 경험적인 측면이 서로 상반된다고는 생각하지 않았지만, 아리스토크세노스가 명확한 수적 비율로 이런을 제시하지 않은 것도 비판했다.
『하모니론』에서의 주제는 다음과 같이 다양하다: 하모니 이론의 원칙과 목적(I, 제1〜2장), 음향학(I, 제3〜4장), 음정이론(I, 제5〜11장), 테트라코드의 유형(I, 제12장 중 일부), 헬리콘(helicon, 모노코드의 일종: II, 제2장), 옥타브의 유형(II, 제3장), 대완전체계와 선법의 ‘자리옮김’ 형태(II, 제4〜11장: 아리스토제누스 비판), 모노코드(II, 제12〜13장), 실제로 사용되는 테트라코드의 혼합 유형(II, 제14〜16장), 15줄의 모노코드(III, 제1〜2장), 음과 영혼과의 관계(III, 제3〜7장), 음과 하늘의 별들과의 관계(III, 제8〜16장).
(1) 음정이론: 프톨레마이오스는 피타고라스 학파의 음정이론에서 옥타브보다 큰 음정과 옥타브보다 작은 음정(즉, 복합음정과 단순음정)이 다르게 취급되는 것을 비판했다. 즉, 4도가 협화음정인 반면, 11도가 (x+1): x 형태(예: 진동수의 비 3:2, 4:3)나 배수 관계로 되어 있지 않다는 이유 때문에 불협화음으로 취급되는 것은 잘못된 판단이라는 것이다. 그는 또한 단순한 음정비율을 위해 온음에 대한 서로 다른 수적 비율을 -테트라코드에서의 각 음들 사이의 음정비율로- 제시했으며, 그런 과정에서 아리스토크세누스의 4도(2개의 온음+반음)와 옥타브의 크기(6개의 온음)에 대한 주장도 반박했다.
(2) 선법이론
① 선법의 유형들: 선법은 특정한 음정구조를 갖춘 음계를 말한다. 프톨레마이오스는 이들 선법을 우선 고정된 음높이가 아니라 상대적 음정 관계(예: 온음-반음-온음…)로 표시하고 있는데, 이것들을 편의상 임시표가 없는 가장 단순한 형태로 옮겨보면 다음과 같다.

② 선법의 자리옮김: 프톨레마이오스의 선법이론에서 다루어진 선법의 소위 ‘자리옮김’ 개념은 당시의 이론적 음역인 '대완전체계'와 실제 연주의 음역이 다른 데서 비롯된 것이다. 즉, a1 〜 A의 두 옥타브의 음역 가운데 당시 연주에서 실제로 사용되었던 음역은 (그 당시의 악기들을 통해서도 알 수 있듯이) 사실 가운데 부분인 e1 〜 e의 한 옥타브에 불과했다('소완전체계': Lesser Perfect System).
이 한 옥타브의 음역에서 일곱 선법이 모두 연주될 수 있는 방법은 그 당시 개념으로는 조 율(‘harmonia’ 또는 ‘metabolē’)을 달리 하는 것이고, 이것을 근대적 개념으로 쉽게 표현하면 임시표를 다양하게 사용하여(즉, 조옮김하여) 선법의 음정적 특성을 그대로 살리는 것이다.

e1 〜 e의 온음계적 음계와 일치하는 도리아는 그 당시 가장 대표적인 것으로 취급된 것이다.
③ 메세: 고대 그리스의 옥타브체계에서 ‘메세’(mesē: ‘가운데’)라는 명칭을 갖고 있는 음은 다른 음보다 자주 나타나는 선율의 중심음 역할을 한 것으로 추측되는데, 이러한 기능으로서의 메세는 그리스의 a1~A 음역에서의 중간음인 a음을 말한다.
이런 고정음으로서의 ‘(기능적) 메세’ 이외에, 프톨레마이오스는 (이론가들 가운데 유일하게) 각 선법에 고유한 소위 ‘(위치적) 메세’들에 대해서도 논급하고 있다. 이런 메세들은 선법들을 e1 〜 e 옥타브로 자리옮김하는 것과 더불어 선법의 중요성을 강조한 데서 비롯된 것이다. 즉, 당시의 연주음역의 온음계와 일치하는 도리아의 메세는 고정적 메세이기도 한 a음(종지음에서 5도 아래의 음)인 반면, 같은 음역에서의 다른 선법들의 메세는 각각 그들 고유의 음정패턴을 기본으로 하여 만들어낼 수 있는 도리아에서의 메세와 일치한다(이 때의 도리아는 연주음역 밖에 걸쳐 있는 가상적인 것이 된다).
아래의 도표를 보면 이해하기가 쉽다. e1 〜 e 음역의 프리지아에서 그 두 번째 음인 f#음을 한 옥타브 위에도 첨가하여 f#1 〜 f# 음역의 음계로 만들어 보면 이것이 곧 도리아가 됨을 알 수 있다(즉, 이 음계에서의 음정패턴은 도리아의 음정패턴과 같다). 도리아 음계는 종지음에서 완전5도 아래의 음을 메세로 하므로, f#1 〜 f# 도리아의 메세는 b음이 되고 이 음이 바로 e1 〜 e 음역의 프리지아에서 메세의 기능을 갖게 되는 음이다.

리디아의 경우에는, 위의 표에서처럼, f#과 g#음이 옥타브 위로도 적용되어 만들어진 g#1 〜 g# 음역에서 도리아가 나타나게 된다. 따라서 이 도리아의 메세는 g#1음의 5도 아랫음인 c#1음이 되고, 이것이 바로 e1 〜 e 음역에서의 리디아의 메세가 된다. 나머지 선법들의 메세도 이와 같은 방법으로 구할 수가 있다. 각 선법에서의 메세는 다음과 같다.

메세가 이론뿐만 아니라 실제로도 선율의 중심음 역할을 했는지는 현존하는 음악만 가지고는 알 수가 없다.
(3) 조율법: 프톨레마이오스는 그 자신을 비롯한 여러 그리스 이론가들의 조율이론을 가장 폭넓게 밝힌 인물이다. 그가 피타고라스 조율법을 보완할 수 있는 것으로 언급한 ‘디아토논 신토논’(그.Diatonon syntonon, 영.Diatonic Syntonic)은, 디디모스(Didymos, 1세기에 활동)의 조율이론(디아토논)을 반영한 것으로서, 중세 말부터 발전하는 순정율의 기원으로 불리기도 하는 것이다. 그러나 디아토논 신토논은 테크라코드에 관한 것으로서 옥타브음계의 3도와 6도음정의 조율에 초점이 맞추어져 있는 순정율과는 아직 상당한 거리가 있다.
① 피타고라스 조율법: 프톨레마이오스 등을 통해 알 수 있는 피타고라스 조율법은 고대 그리스에서 사용된 최초의 체계적인 조율법으로서 엄격한 수학적 원칙을 기본으로 한다. 즉, 이 조율법에 근거한 온음계나 반음계는 주어진 음으로부터 순정5도의 진동수 비율인 3:2(순정음정은 조율법에서 최소공배수가 작은 정수들의 비율로 된 협화음정을 말한다)씩 연속적으로 조율해나간 음들을 옥타브의 음정비율을 이용하여 한 옥타브 안으로 모아들인 것이다.
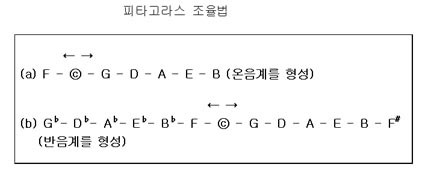
그 모아들이는 과정을 D음을 한 예로 가지고 수학적으로 설명을 해보면 다음과 같다. C를 출발점으로 볼 때 D는 그 음으로부터 5도씩 두 번 상행한 음에 해당하므로, 그 음정비율은 3/2 × 3/2 = 9/4가 된다. 이 D음의 한 옥타브 아래에 있는 음의 음정비율을 구하려면(즉, C와 온음관계인 D음을 구하려면) -옥타브의 음정비율이 2배수로 이루어지므로- 그 음정비율을 2로 나누면 된다(즉, 9/8).
② 디아토논 신토논: 피타고라스 조율법에서는 장3도 비율이 81/64로 복잡한데 비해, 디아토논 신토논에서의 장3도의 음정비율은 5/4로 단순하다는 이점을 갖고 있다(사실 그 차이는 미세하다: 80/64 = 5/4). 그러나 이 조율법은 동시에 온음의 음정비율이 동일하지 않은 모순을 안고 있다. 즉, 피타고라스 조율법에서의 온음비율은 모두 9/8인 반면(9/8 × 9/8 = 81/64), 디아토논 신토논에서는 10/9와 9/8로 나뉘어 있다(10/9 × 9/8 = 5/4). 즉, 디아토논 신토논에서의 테트라코드(디아토닉 테트라코드)는 10/9 - 9/8 - 16/15의 음정비율로 이루어져 있다(디디무스의 디아토닉 테트라코드에서는 앞의 두 음정비율의 위치가 바뀌어 있다: 9/8 - 10/9 - 16/15). 두 경우 모두 테트라코드의 음정크기는 4/3(9/8 × 10/9 × 16/15 = 4/3).
디디무스-프톨레마이오스의 조율이론은 피타고라스 조율법을 비판적으로 보완한 것이지만, 그 기본 원리는 후대에 가서야 빛을 보게 된다. 즉, 좁은 음역과 완전음정들을 기본 음정으로 사용한 중세 시대에는 이 조율법이 한 동안 큰 문제없이 계속 수용될 수 있었다. 뿐만 아니라, 이 조율법은 사실 18세기까지도 그 영향력을 완전히 잃지는 않는다.

