헥사코드(라, Hexachordum. 도.영.hexachord, 뜻: "여섯 음", 번역어: 6음렬)
계명창의 효시가 되는 중세의 이론. 헥사코드는 오늘날의 계명창 명칭으로는 도, 레, 미, 파, 솔, 라에 해당하는 여섯 음을 말한다. 이 6음렬은 11세기 귀도 다렛쪼(Guido d'Arezzo)가 창안했다("미지의 성가에 관한 서한"Epistola de ignotu cantu 1028). 각 음들의 명칭은 원래 Ut(오늘날은 Do로 바뀜), Re, Mi, Fa, Sol, La이었다. 헥사코드의 음절 명칭들은 16세기에 Ti(또는 Si)로 덧붙여져 오늘날의 도레미파솔라시도가 되었고, 솔미사치오(solmisatio) 또는 솔페지오(이.solfegio, 프.solgège)라 불린다. 솔페지오는 오늘날도 이태리와 프랑스에서 아직도 사용된다. 프랑스에서는 Do음이 아직도 Ut로 불린다.
귀도 다렛쪼는 당시 8세기 경부터 전해오던 요한찬가(Ut queant laxis)의 가사에 도리아 선법의 선율을 붙였다. 이 때 여섯 구절이 각각 c, d, e, f, g, a(Ut, Re, Mi, Fa, Sol, La)음으로 시작하게 하였고, 이들 음에 해당하는 가사의 음절들을 뽑아 6음렬의 명칭으로 사용하였다. 이 6음렬의 중심 부분인 e와 f 사이는 항상 반음이고 나머지는 모두 온음 간격으로 구성되어 있어서, 이를 기억하면 쉽게 악보를 읽을 수 있었다.

귀도의 헥사코드 체계는 B음이 있고없고에 따라 세 가지의 기본 유형으로 구분된다.
①"자연스런"(hexachordum naturale) 헥사코드: C음에서 시작하는 것으로 B음(Fa의 반음 내림)이 포함 안된 것, 아래 도표의 초록색.
②"연한"(hexachordum molle) 헥사코드: F음에서 시작하는 것으로 (F음과 B음 사이의 증4도를 피하기 위해) Bb(Fa를 반음 내림)음을 포함하는 것. 내림표의 둥근 모양에서 그 이름이 유래했다. 아래 도표의 파랑색.
③"강한"(hexachordum durum) 헥사코드는 G음에서 시작하는 것(이 이름도 임시표 모양에서 유래). 아래 도표의 빨강색.

헥사코드는 전조 부분도 쉽게 읽을 수 있도록 했다. "전조"는 오늘날의 용어이고 당시는 이를 Mutation(변환)이라 불렀다. 예를 들어 Fa를 Ut로 "변환"하여 부르면 전조 부분을 쉽게 노래할 수 있었다.
헥사코드는 지도자의 손을 보고 쉽게 노래할 수 있도록 손바닥의 일정 부분을 각각의 음높이와 연결시켰다(아래 그림 참조: "귀도의 손") 손바닥에 정해진 음들은 절대적 음높이였고, 6음렬의 음높이는 상대적인 것이었다.
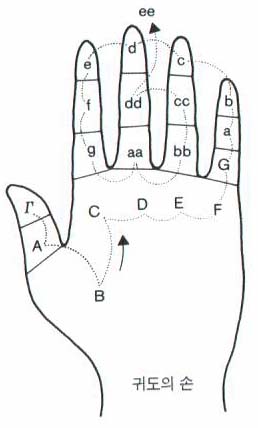
헥사코드를 창안한 귀도는 헥사코드란 용어를 사용한 바가 없으며, 이론적으로 체계화시키지도 않았다. 체계화는 후대의 이론가들에 의해 이루어졌다. 단, 그의『작은 학문』(Micrologus,1026년경)에서 보는 선법의 종지음 자리들(d - g)에 대한 설명과 ‘선법의 음도’(Modes of the Degrees)에 관한 논의를 헥사코드 이론의 뿌리로 보는 견해가 있기는 하다. 실제로 귀도 이후의 헤르만누스 콘트락투스(Hermannus Contractus 또는 Hermann der Lahme 또는 Hermann von Reichenau, 독일, 1013-1054) 등은 선법 종지음들의 결합을 테트라코드로 보고 그 양쪽에 온음을 하나씩 붙여 만든 6도를 헥사코드로 설명함으로써 선법과 헥사코드를 이론적으로 연결하려는 시도를 한 바 있다. ‘선법의 음도’는 선법의 종류에 상관없이 사용 빈도수가 높은 음들에 대한 논의이다. 즉, 정격선법의 경우, (매우 실용적인 측면에서) 세부적인 종류에 상관없이 전형적으로 쓰이는 음도는 c음 〜 a음이며, 변격선법의 경우는 역시 그 종류에 상관없이 g음 〜 d음이라는 것이다. 전자의 음역이 그의 헥사코드 창안에 기초가 되었는지는 알 수 없으나, 결과적으로는 일치한다.
헥사코드 이론에 대한 언급은 18세기 전반 경까지 나타나지만, 다른 한편으로는 이미 15세기부터 옥타브 계명음계가 보다 실용적인 것으로 제안되기 시작한다.[스페인의 바르톨로메오 라모스 드 파레야(Bartolomeo Ramos de Pareia, 1440경-1491 이후)가 쓴『음악의 실제』(Musica practica, 1482).]
귀도 이후의 이론가들에 의해 논급되는 헥사코드의 핵심 이론들은 다음과 같다.
C, F, G음으로 시작하는 헥사코드들이 체계적으로 제시되는 것은 13세기에 이르러서이다. 당시의 한 이론서에서 발췌된 예를 보면, 귀도의 이론서에서 처음으로 논의된 바 있었던 G - dII 음역에 세 종류의 헥사코드가 도합 7개로 나열되어 있다. 또한 하나의 음이 두 개 또는 세 개의 계명을 갖고 있는 경우도 있음을 알 수 있는데, 선율의 문맥에 따라 그 중의 하나로 불릴 수 있었던 것이다. 이후 13세기 말에는 그 음역이 위로 온음 확장되어(G - eII ) 마지막 상행 헥사 헥사코드인 G 헥사코드도 6음을 완전하게 갖추게 된다[히에로니무스 데 모라비아(Hieronymus de Moravia, 1272-1304경 활동)의 저서(Tractatus de musica)에 처음 등장].
중세 이론가들의 헥사코드에 대한 설명 가운데는 "변환"도 포함된다. 이것은 선율의 음역이 6도 이상이거나 B음이 B♭음으로 또는 그 반대로 바뀌게 되는 경우에 일어나게 된다. 변환의 좋은 위치는 양쪽의 헥사코드에 속해 있는 음이 반복되는 곳이다. 이 때, 뒤의 반복음을 새로 오는 헥사코드의 계이름으로 부르면 되는 것이다. 변환에 대한 설명은 14세기에야 나타나는데, 이와 관련하여 ‘코니웅타’(라.coniuncta: ‘연결된 것’이란 뜻)란 용어가 등장하기도 한다. 코니웅타는 헥사코드의 변환 가운데, 특히 f♯, c♯, e♭, a♭ 등의 반음이 포함된 것을 의미한다. 이와 같은 의미는 헥사코드가 이제 C, F, G음만이 아니라, 임시표에 의해 이론적으로 어떤 음에서도 시작될 수 있음을 시사한다.
참고문헌
Guido d'Arezzo: Epistola de ignotu cantu 1028. 한국어 번역본: 「미지의 성가에 관한 서한」(번역: 이요한) →『서양음악사 원전』(스트렁크 편집, 서울대 서양음악연구소 번역, 2002) , 211-214쪽.
G. G. ALLAIRE: The Theory of Hexachords, Solmization and the Modal System, Musicological Studies and Documents XXIV, 1972.
김미옥: 중세음악 역사 이론, 심설당, 2005.
음악은이, 음악춘추사, 2002.
등록일자: 2007-04-19
김미옥/홍정수

